The fundamental experience which objective experience itself
presupposes is the experience of the Other. It is experience par
excellence. As the idea of the Infinite goes beyond Cartesian
thought, so is the Other out of proportion with the power and
freedom of the I.¹

In this discussion I would like to use a rather mundane notion in physics and geometry to try to nuance out what I think is an important difference in common modes of our understanding and orientation to reality. I would like to bring out an equivocation which is a confusion that covers over an essential difference into an abstract habit of thinking. This habit is derived from a dominate, historically conditioned, leveling over of radical breaks in our notions of what ‘is’. The ancient Greeks did not have the modern ‘luxury’ of this imposed abstraction in reflecting on what ‘is’. More to the point, they had the notion of phusis² which embodied the ancient, archaic notion of ‘growth’ also found in other ancient cultures. In this sense ‘growth’ ranged from what Heidegger phrased ‘what shows itself’ and in my estimation the radical rupture of alterity which imposes necessity from other than its showing. ‘Growth’ in this sense is encounter and exteriority. This approach will try to use some quite rudimentary assumptions in science to tease out these philosophical underpinnings.

In geometry there is the abstract notion of a point. The question which brings existential import to a point (i.e., what ‘is’ a point?), is non-sensical. A point does not exist. We may say that it is infinitesimally small. Perhaps we could say that it has no dimension, zero dimensional. A specific case of a point could be a singularity. From what physicists tell us about a black hole we must concede that it ‘is’ a point in its most extreme form. Physicists are very confident that black holes exist and that they result in a singularity, a radical tear in time-space, an infinitesimally small point. As such, the singularity is a mathematical impossibility. Philosophically, we would say that a black hole is a mathematical contradiction; it is necessarily false. However, let’s notice the shift we have just announced.

We started suggesting that a point is an abstract mathematical concept does not exist empirically; it has no dimension. Zero dimensionality is not conceivable. And yet, we seem to have empirical evidence that a point can exist in a black hole. We may defer this contradiction as a lack of knowledge to be resolved in an unknown, unforeseen, moment in the future. As such, we acknowledge that we must currently leave this matter as a paradox³. Such a point is an argument to ignorance and only defers the immediacy of an answer which now faces us in this discussion. The argument to ignorance does not provide resolution only gives permission to ignore a persistent question.

Let us note that we have attributed qualities to the ‘point’ as “infinitesimally small” and as highly certain that it empirically exists in a black hole. We cannot resolve these conflicting notions in the light of rationality. They must remain ‘infinitely’ recoiled in upon themselves without coming into the light as aufheben (i.e., without being “lifted up”, ” abolished”, “canceled”, “suspended”, or “sublated”). This infinite impossibility can only be preserved in its inability to be able to transcend or exceed itself. It remains as an obligation we cannot refuse in its stark, declarative unmediated, absolute self-contradicted specificity. However, we can ignore it altogether and the direct question it essentially poses to the ‘light’ of knowledge.

In this case ‘light’ is taken hold of by the Latin notion of ratio which was the interpretation of the ancient Greek word logos. Specifically for this treatise, in terms of Heraclitus’ refinement as ‘giving account’, as ‘justice’ and ‘recompense’. ‘Light’ in this sense is the field of sight where idea is nudged towards resolve, towards answer and accountability. Dialectic can only exist in this clearing, this region already ready for an answer. In this sense, idea remains in itself; it encloses itself as Truth. Sight lays hold of its object without referring to abstractions; it simply sees. Therefore, by ‘light’ I mean the Idea as remaining within itself. In analogous terms of physical science, such a notion as Idea remaining in itself might be referred to as an isolated system – no interaction with matter or energy outside of itself. In Hegelian terms we might even venture further that anything ‘outside’ of Idea is still Idea and therefore an absolute impossibility except as yet another idea. It forever must get re-appropriated into the isolation of its Truth.

Additionally, note here that falsity also remains in itself as a deprived mode of Truth often erroneously taken as an opposite. Falsity always resolves itself essentially in contradistinction to Truth. Truth can only assert itself in its privation, its lack as error and thus, remain in itself. For example, light is only known through darkness, good is only known through bad, etc.. Only by the essential ‘not’ can Truth make its eternal claim. Truth remains in logos as an essential condition for sight, for logic to assert its priority in its isolation. Specifically, this condition we refer to as being or ontology as the essential pillar of language, the copula which founds all possibilities of writing. Ontology in this case is what sifts and retains identity from Hesiod’s random chaos (χάος⁴), what must and can only show itself in the clearing of light.

The notion of singularity, as a mathematical point, cannot be seen or conceived and yet ‘is’. Therefore this notion cannot remain within itself. When taken as ‘sight’ a singularity can only be pushed away from itself such that sight cannot contain or make sense of its object. In distinction to Truth, that which remains in itself as the march of being, we have an absolute paradox which somehow still retains the yawning gap of Hesiod, χάος⁵. This essential difference should not be lost in the notion of negation. Negation resolves and levels off this difference by virtue of what it negates. It implies a positive term which then must necessarily be what is negated. The difference I am trying to bring out is that lack of a positive term to negate. This paradox, simultaneously ‘is’ and ‘is not’ perhaps gleamed in the ancient Greek notion of chaos. The paradox cannot be contained on the ‘not’ of negation without doing an injustice. We must open the isolation of this logocentric system which only must remain in itself. With this in mind, lets reflect on what we might think of as qualities of an idea which cannot remain within itself but necessarily points to an unseen, essentially undiscoverable, externality.

Of the idea of infinity, Renes Descartes writes:

Nor should I imagine that I do not perceive the infinite by a true idea, but only by the negation of the finite, just as I perceive repose and darkness by the negation of movement and of light; for, on the contrary, I see that there is manifestly more reality in infinite substance than in finite, and therefore that in some way I have in me the notion of the infinite earlier then the finite⁶

Descartes recognized that the idea of infinity is very different from other ideas. While at times he thought of infinity in terms of negation he also thought of infinity as “manifestly more” and in some way “earlier”. The idea of infinity cannot be shown in the light of the idea of an object like a chair for example. To tease this out further, the idea of infinity cannot rest in itself but can only point away from itself without pointing to a thing, a positive term. The idea overflows itself without resolve, without regard to what it ‘is’.

Calculus is the mathematics of infinity. It can describe infinities in terms of ‘limits’ as infinity approaches a limit. It can describe infinities as ‘converging’ and ‘diverging’. Let’s take the function, ‘1/x’, where x goes from minus infinity to plus infinity (see chart below). You can see on the chart that from -1 to minus infinity the solution reaches a limit of zero. From -1 to just below zero the solution goes to minus infinity. Likewise, from 1 to infinity the solution reaches a limit of zero. From 1 to just above zero the solution goes to infinity. At zero 1/X is undefined.

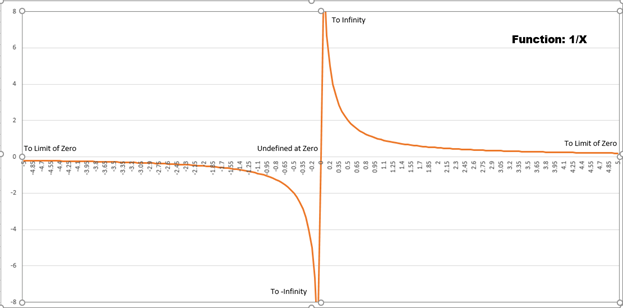
Therefore, while we have not gained any insight into the notion of infinity, we have described qualities around the, ever exceeding itself, notion of infinity in certain circumstances. Likewise, while we cannot resolve the previously discussed dilemma of the geometrical point as an impossible singularity, we can point out certain behavior around that impossibility. This behavior nevertheless does not undo the Gordian Knot except by leveling it over with negation or ignoring it altogether. This paradox then weaves itself in the field of light without ever being consumed by the light.

From henceforth, we shall we refer to specific reductions such as the function ‘1/x’, converging and diverging on a limit of ‘1’ as providing a degree of diachronic ‘closure’ to the odd idea of infinity; that is, standing alongside the rupture of the idea of infinity without overtaking it. In this type of behavior infinity taken up in history and easily lost in negation and ignore-ance. Likewise, the abstract and inconceivable idea of the point as infinitesimally small, embodied in the impossible contradiction of a black hole, supplements the idea with an existential empiricism that adds a degree of semblance as closure. These further qualifications bring relevance to an inherit excess to the idea of infinity without covering over the radical rupture of the idea. Likewise, we shall refer to qualities which refuse resolution (such as zero dimensional, infinitesimally small, etc.) as moving towards an un-addressable exteriority which opens towards an unbridgeable tear in the interiority of ideas or self-enclosed-ness.

This openness does not open towards a Heideggerian kind of clearing but rather imposes itself in its absolute impossibility which cannot be denied. Interesting enough Heidegger writes:

“Death is the possibility of the absolute impossibility of Dasein [human being, the ‘there’ of being]. Thus death reveals itself as that possibility which is one’s ownmost, which is non-relational, and which is not to be outstripped”.⁷

In my estimation for example, the absolute impossibility of a point which cannot exist and yet must as a singularity does not belong to Dasein or even Being but to what Levinas refers to as otherwise than Being. The rupture I have spoken of is radical tear which cannot be resolved either in Being or Hegel’s Idea. It cannot be taken hold of but must always remain out of reach, without mediation, without relating in any way to one’s ownmost (which brings into question how death can be related to “one’s ownmost AND non-relational).

The tendency to closure of paradox may provide conditional qualities around which we can, in a limited fashion, provide some resolution around a logical impossibility without abolishing the necessary impossibility it enshrouds. To some extent openness provides us a specificity in the bare name such as the word ‘infinity’ which can be pragmatically useful in service to such qualities previously discussed but ultimately fail in their inability to find any complete closure within themselves with their sheer imposing impossibility. The tear in the fabric of rationality is not overtaken by rationality. It is not snuffed out by the forceful wish of dialectic and aufheben. Nor is it tamed by the totality of Being. For the early Greeks it remained as,

Tell me all of this, you Muses who have your homes on Olympus, from the beginning [archê, ἀρχῆς], tell who first of them (the gods) came-to-be [genet’, γένετ᾽].
First of all Chaos came-to-be [genet’, γένετ᾽]⁸

…for Levinas and the gift of Judaism, the provocation of the Other.

 

_________________

¹ From “Signature”, an essay in:
“DIFFICULT FREEDOM”
Essays on Judaism
Emmanuel Levinas
Translated by Sean Hand
English translation published 1990 by
The Johns Hopkins University Press
2715 North Charles Street
Baltimore, Maryland 21218-4363
www.press.jhu.edu
Johns Hopkins Paperbacks edition, 1997
9 8 7 6 5 4 3

² Ancient Greek

From φῠ́ω (phúō, “grow”) +‎ -σῐς (-sis).

Noun: φῠ́σῐς • (phúsis) f (genitive φῠ́σεως); third declension

See also φύσις in Liddell & Scott (1940) A Greek–English Lexicon, Oxford: Clarendon Press

³ paradox – a seemingly absurd or self-contradictory statement or proposition that when investigated or explained may prove to be well founded or true

⁴ Philosophy Series 4 – The Pre-Socratics – Hesiod

⁵ Philosophy Series 4 – The Pre-Socratics – Hesiod

⁶ Renes Descartes, “Meditations on First Philosophy”, Third Meditation

⁷ Martin Heidegger, “Being and Time”, 53: 307

⁸ Hesiod, Theogony